Many NP research areas require the analysis of complex datasets or theoretical calculations in order to uncover underlying physical distributions or parameters, so-called Inverse Problems. Examples of such studies being carried out in the NSD include the mapping of natural and anthropogenic radiation environments using radiation detectors, measurements of the mass and fundamental nature of the neutrino, and determination of the properties of the Quark-Gluon Plasma (QGP) from collider data.
The tool of choice to solve Inverse Problems is Bayes’ Theorem. However, the application of Bayes’ Theorem in these areas is computationally expensive, due either to complex simulations (QGP, neutrino detector simulations) or too many parameters in the problem (radiological mapping, neutrinoless double beta decay). Approaches based on Machine Learning (ML) are needed for their tractable solution with currently available computing. A key element in any physics analysis is the specification of uncertainty, which is especially challenging for ML-based solutions of Bayes’ Theorem.
The Bayesian Uncertainty Quantification (BUQ) project is a DOE-supported collaboration of physicists and data scientists from the NSD, UC Berkeley, and other universities, to develop ML-based solutions to the Inverse Problem for QGP, neutrino, and radiological mapping studies. This mix of quite different projects was chosen deliberately, to explore their commonalities and differences in order to search for general ML-based solutions, with emphasis on uncertainty quantification. Common tools have indeed been identified, using for instance Transfer Learning and Multi-fidelity Learning, with comparison of their application to the different sub-projects ongoing.
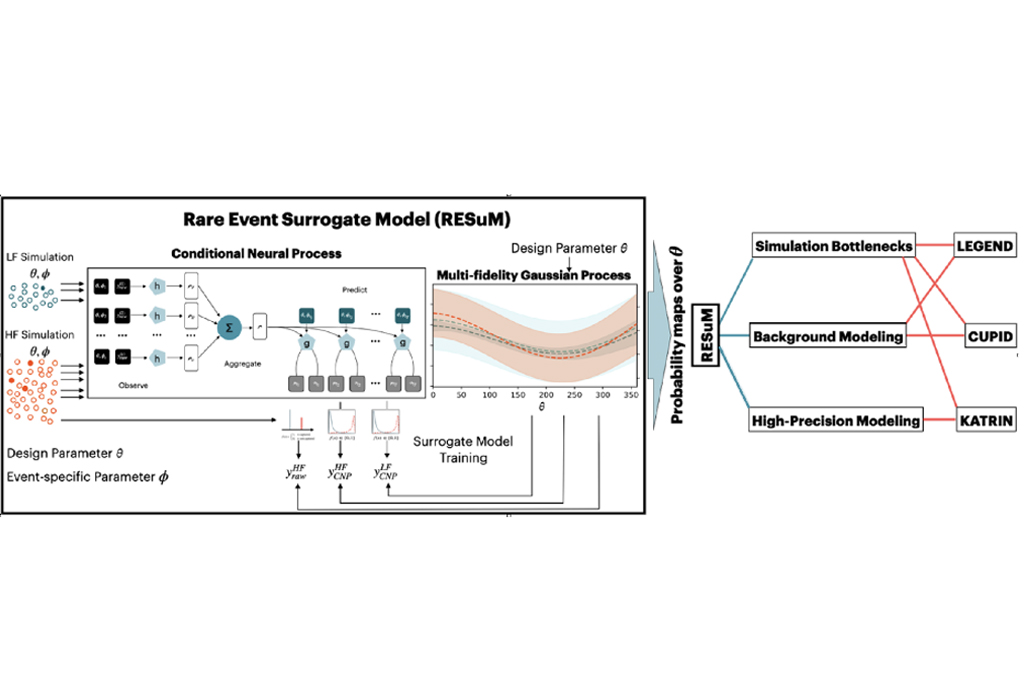
A significant recent development in the neutrino sub-project is the development of the Rare Event Surrogate Model (RESuM) for physics detector design optimization under Rare Event Design (RED) conditions. RESuM utilizes an ML tool called the Conditional Neural Process (CNP) model to efficiently encode detailed detector response data into a Multi-Fidelity Gaussian Process calculation. The team applied RESuM to optimize neutron shielding designs for the LEGEND neutrinoless double-beta decay experiment, identifying an optimal design that reduces the neutron background by a large factor while using less than 5% of the computational resources required by traditional methods. The RESuM algorithm has broad potential for efficient simulations in many areas of NP. This work was recently published and presented as a “spotlight” talk by NSD Postdoc Ann-Katherin Scheutz of the NSD at the prominent International Conference on Learning Representations (ICLR2025).
Architecture of the RESuM model and overview of connections with different neutrino projects.
Members of the BUQ Project in the NSD are Peter Jacobs, Lipei Du, Raymond Ehlers, and Florian Jonas (QGP), Jayson Vavrek and Lei Pan (radiological mapping), and Yury Kolomensky, Alan Poon, Daniel Mayer and Ann-Katherin Scheutz (neutrinos). Jacobs is the project PI, while Kolomensky, Poon, and Vavrek are NSD co-PIs.
